Learning Sparse Graphs for Functional Regression using Graph-induced Operator-valued Kernels
Learning to predict functional output from a suitable input is characterized as a functional regression problem, which aims at learning a function-valued function \(F:\mathcal{Z}\rightarrow\mathcal{Y}\), where \(\mathcal{Z}\) is an appropriate input space and \(\mathcal{Y}\) is an output space of functions.
In many scenarios, multiple inputs decide the value of an output, which gives rise to functional regression problems of the form \(F:\mathcal{Z}^p\to\mathcal{Y}\), where \(p\) is the number of inputs considered.
Even more interesting is the case where interactions among the \(p\) inputs can be used in a precise manner to predict \(y\in\mathcal{Y}\).
In particular, we consider \(\mathcal{Z}\) to be a space of functions, hence learning a map \(F:\mathcal{Z}^p\to\mathcal{Y}\) is called a many-to-one function-to-function regression problem.
Without loss of generality, we refer to this many-to-one function-to-function regression problem as the functional regression problem considered throughout this paper.
Applications of this type of problems can be found in weather forecasting where different weather parameters in stations measured at multiple timepoints across a month can be characterized as functional inputs used to determine the average rainfall as a time-varying function in that month.
Similarly, emissions from a factory in a day can be predicted as a function of time, based on the functional data obtained from readings of different components involved in the manufacturing process at different timepoints in that day.
In sports analytics, the movement data of different players throughout the game can let us know the influence of a particular strategy in ball possession/movement as a functional output over the duration of the game.
Thus in all these applications, we notice situations where a set of input functions interact to produce an output function.
Even though digital data is discrete, systems where the inherent data produced is smooth and continuous by nature, can be modeled as functions over a suitable domain to leverage the variations based on that domain.
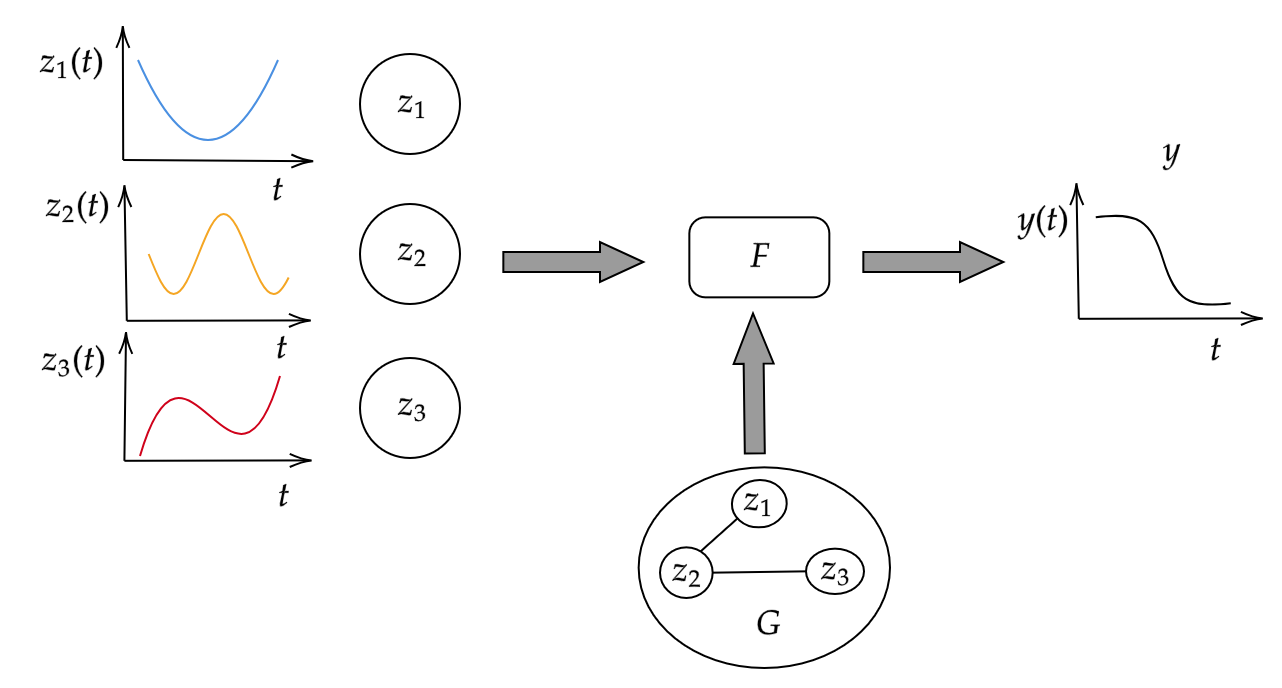
Consider a simple functional regression problem illustrated in , where input functions \(z_1,z_2,z_3\in\mathcal{Z}\) denote the atmospheric pressure measurements of 3 nearby weather stations and the output function \(y\in\mathcal{Y}\) denotes the average temperature of the region, throughout a particular day.
For predicting \(y\), considering the input functions \(z_1,z_2\) and \(z_3\) without any relation among them may be restrictive as inherent relations between the input functions may dictate the generation of \(y\).
In order to capture interactions among \(z_1,z_2,z_3\), we introduce a graph structure \(G\) between \(z_1,z_2\) and \(z_3\) in , where the nodes of \(G\) represent \(z_i\)'s and the edges depict potential relations among them.
The graph structure \(G\) will be useful in representing the influences and inter-relations among \(z_i\)'s, which can be useful in the prediction of \(y\in\mathcal{Y}\) using \(F\).
We propose a framework for combining the impact of \(z_1,z_2,\dots,z_p\) with the additional information of \(G\) to predict \(y\).
In determining the output function \(y\), the graphical structure \(G\) on the input functions may be known from domain knowledge and can possibly be directly incorporated to learn \(F\).
A more interesting case is when \(G\) is unknown and needs to be learned along with \(F\).
Learning the graph structure \(G\) would help to discover interactions among \(z_i\)'s which facilitate predicting \(y\).
When the number of input functions \(z_1,z_2,\dots,z_p\) grow larger, the associated graph \(G\) might also become dense with many edges, and incorporating such dense \(G\) might lead to computational difficulties and would also lead to spurious connections/edges which lack interpretability.
Thus, learning a sparse graphical structure \(G\) on input functions becomes instrumental in understanding the significant relationships that drive the functional regression problem to predict the output function.
To solve this regression problem with \(p\) input functions and a corresponding output function, we propose a graph-induced operator-valued kernel obtained by imposing a graphical structure describing the inter-relationships among the \(p\) input functions.
When the underlying graphical structure is unknown, we propose to learn an appropriate Laplacian matrix characterizing the graphical structure, which would also aid in learning the map \(F\).
We formulate a learning problem using the proposed graph-induced OVK and devise an alternating minimization framework to solve the learning problem.
To learn \(F\) along with meaningful and important interactions in the graphical structure, a minimax concave penalty (MCP) [Ying et al., 2020] is used as a sparsity-inducing regularization on the Laplacian matrix.
We further extend the alternating minimization framework to learn \(F\), where each of the \(p\) constituent input functions and the output function are multi-dimensional.
We design an efficient sample-based approximation algorithm to scale the proposed algorithm to large datasets.
Further, we provide bounds on generalization error for the map obtained by solving the proposed learning problem.
An extensive empirical evaluation on synthetic and real data demonstrates the utility of the proposed learning framework.
Our experiments show that simultaneous learning of \(F\) along with sparse graphical structure helps discover significant relationships among the input functions and motivates the interpretability of such relationships driving the regression problem.